Complex analysis is complex. Though it has some cool results that you cannot find in real analysis ( •_•)>⌐■-■.

The main focus for this class is the study of "holomorphic" functions, functions that are differentiable in the complex sense. We will begin with basic definitions, then move on to path integrals, power and Laurent series and end the class with the very cool results. One interesting property of holomorphic functions is that they can be defined uniquely by a few points on a domain. This is the order of topics we will follow as this is the natural order of how our results arise.

In this section we will cover fundamental definitions and properties of complex analysis. Feel free to skip the proofs here, they're pretty boring.

Let us state some elementary complex definitions:

• $z = x + iy$, $z \in \C, x,y \in \R$
• $e^z := e^xe^{iy} = e^x(\cos y+i \sin y)$
• $\ln z := \ln|z|+i\arg z$, $0\leq \arg z < 2\pi$
• $z^w := e^{w\ln z}$
• $\Arg z := \set{\arg z+2\pi m, m \in \Z}$
• $\Ln z := \ln|z| + i\Arg z$
• $\sin(z) = \frac{e^{iz}-e^{-iz}}{2i}$
• $\cos(z) = \frac{e^{iz}+e^{-iz}}{2}$

We say that a function $f$ if $\C$-differentiable at $z_0$ if there exists some $f'(z_0) \in \C$ with

We can equivalently define complex differentiability using Cauchy-Riemann equations with the proof idea of comparing the above definition of complex differentiability with differentiability of functions $f:\R^2 \to \R^2$. Say a function $f: \C \to \C$, $f(x,y) = u(x,y) + iv(x,y)$ is $\C$-differentiable at $z_0=x_0+iy_0$ if $f$ is $\R$-differentiable and the Cauchy-Riemann equations hold

The Jacobian matrix $J_f(z_0)$ is used to represent the information of all the partial derivatives of $f$ at $z_0$

A domain is a set $D \subset \C$ which is open and connected.

If $D$ is a domain, a function $f:D \to \C$ is called holomorphic (on D) if it is $\C$-differentiable at every $z \in D$. Write $H(D)$ as the set of all functions holomorphic on $D$. A function $f \in H(\C)$ is called entire. Fun fact: holomorphic comes from the Greek words ὅλος and μορφή, meaning "entire and "form" respectively.

Some quick facts we can get from this is that $H(D)$ is a vector space and even a ring with function addition and multiplications. Moreover, if $D$ is a domain, then $f(D)$ is connected if $f$ is continuous and hence if $f$ is holomorphic. Polynomials are an example of an entire function. We will show later by Liouville's theorem that entire functions are either equal to the zero map or unbounded.

A map $f:D \to G$ for $D,G$ domains is called biholomorphic or a conformal equivalence if $f$ is bijective and both $f$ and $f^{-1}$ are holomorphic. We can find biholomorphic functions with the following theorem which we will prove later.

$\textbf{Theorem 1.1.}$ If $f \in H(D)$ and $f$ is injective, then $G=f(D)$ is a domain. So in this case $f:D\to G$ is biholomorphic.

Let us give explicit biholomorphic functions with this theorem. Define

Then for $\b - \a \leq 2\pi$, the exponential function $e^z \mid_{S_{\a,\b}}$ is injective. So $e^z$ is a conformal equivalence between $S_{\a,\b}$ and $A_{\a,\b}$. Similarly, $\ln \mid_{A_{0,2\pi}}$ is bihilomorphic with inverse $e^z \mid_{S_{0,2\pi}}$. Although we have $e^{\ln(z)} = z$ for all $z \in \C$, we only have $\ln(e^z) = z$ if $0 \leq Im(z) < 2\pi$. Exercise: find a conformal equivalence from $\C\setminus\R_{< 0}$ to $S_{-\pi i, \pi i}$.

A path is a continuous function $\g:[0,1] \in \C$. A path is smooth at $t_0\in(0,1)$ if $\g'(t)\not=0$ (don't get this mixed up with the other definition of smooth meaning having continuous derivatives). A smooth path through $z_0 \in \C$ is a pair $(\g,t_0)$ where $\g$ is a path that is smooth at $t_0$ and $\g(t_0) =z_0$. This basically says that a path does not stop at any time between 0 and 1.

A function $f$ is conformal at $z_0$ if

1. $f$ is $\R$-differentiable at $z_0$
2. $J_f(z_0)$ is invertible
3. if $(\g,t_0)$ and $\tilde{\g},\tilde{t_0})$ are two smooth paths through $z_0$, then the oriented angle from $\g'(t_0)$ to $\tilde{\g}'(\tilde{t_0})$ is the same as the one for $(f\circ\g,t_0)$ and $(f\circ\tilde{\g},\tilde{t_0})$

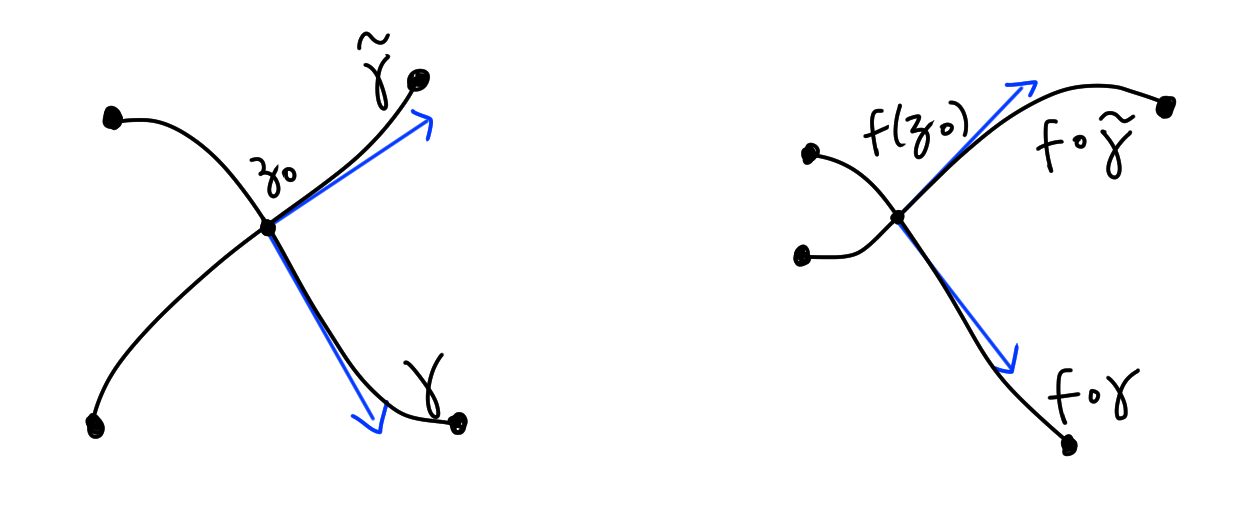
We have a theorem which gives an equivalent definition of conformal. However, we only prove one direction now with Proposition 1.3 and leave the other direction for later.

$\textbf{Theorem 1.2.}$ A function $f$ is conformal at $z_0$ if and only if $f$ is $\C$-differentiable at $z_0$ and $f'(z_0) \not=0$.

$\textit{Proof.}$ Exercise to show $1 \iff 2$ and $2 \iff 3$. $\Box$

Then we have a stereographic projection $\pi:S^2 \to \hat{\C}$ with $\pi(0,0,1) = \infty$ and $\pi(x,y,w)$ $=$ $(\frac{x}{1-x},\frac{y}{1-w})$ for $w\not=1$. Its inverse is given by $\pi^{-1}:\hat{\C} \to S^2$ with $\pi^{-1}(\infty) = (0,0,1)$ and $\pi^{-1}(x,y)$ $=$ $(\frac{x}{1+|z|^2},\frac{y}{1+|z|^2},\frac{|z|^2}{1+|z|^2}).$ This gives us a "conformal identification" between $\hat{\C}$ and $S^2$.

Now let a domain $D \subset \hat{\C}$. Say that $f:D \to \hat{C}$ is $\C$-differentiable/conformal at $z_0\in D$ if

• Case 1: $z_0\in\C,$ $f(z_0)\in\C.$ Use old definitions.
• Case 2: $z_0=\infty,$ $f(z_0)\in\C.$ Apply usual definitions to $f \circ \frac{1}{z}$.
• Case 3: $z_0\in\C,$ $f(z_0)=\infty.$ Apply usual definitions to $\frac{1}{z} \circ f$.
• Case 4: $z_0=\infty,$ $f(z_0)=\infty.$ Apply usual definitions to $\frac{1}{z} \circ f \circ \frac{1}{z}$.

This section will cover an interesting set of biholomorphic functions on $\hat{\C}$ with some interesting properties. In fact, the set we will describe will be the set of all possible conformal functions over $\hC$. Given $X = \begin{bmatrix} a & b \\ c & d \end{bmatrix} \in GL_2(\C)$ an invertible 2 by 2 matrix ($ad-bc\not=0$) over $\C$, we can define a function $\lambda_X : \hat{\C} \to \hat{\C}$

Define a set of Möbius transformations by

Note that for $w\not=0$, $wX$ and $X$ correspond to the same function such that $\l_X = \l_Y$ if and only if $Y = wX$ for some $w$. It is possible to show with some elementary algebra a variety of good properties about Möbius transformations.

$\textbf{Theorem 1.4.}$ Let $\l \in \Mob$. Then $\l:\hC\to\hC$ is biholomorphic and conformal at every $ z \in \hC$.

$\textit{Proof.}$ Exercise with lots of cases. $\Box$

$\textbf{Proposition 1.5.}$ Let $X,\tilde{X} \in GL_2(\C)$. Then $\l_X \circ \l_\tilde{X} = \l_{X\cdot \tilde{X}}$.

This latter result induces a group homomorphism $GL_2(\C) \to \text{Conf}(\hC)$, the group of conformal equivalences $\hC \to \hC$ with image $\Mob$ and kernel all nonzero multiples of the identity. Thus, by the first isomorphism theorem we have

$\textbf{Lemma 1.6.}$ Let $\l\in\Mob$. Then $\l$ is either the identity, or has exactly 1 or 2 fixed points in $\hC$.

An example of a $\l$ with one fixed point is a shift $z+1$. An example of a $\l$ with two fixed points is dilation $2z$.

$\textit{Proof.}$ Again proof by cases by noticing that solving $\l(z)=z$ either has one, two or infinite solutions. $\Box$

$\textbf{Corollary 1.7.}$ If $\l,\tilde{\l} \in \Mob$ and there exist 3 distinct $z_1,z_2,z_3 \in \hC$ such that $\l(z_i) = \tilde{\l}(z_i)$ for each $i$, then $\l = \tilde{\l}$. i.e. 3 points define a Möbius transformation.

$\textit{Proof.}$ Writing $\l=\l_X$ and $\tilde{\l} = \l_\tilde{X}$, we have $\l\circ\tilde{\l}^{-1} = \l_{X \cdot \tilde{X}^{-1}}$ fixing three points such that it is the identity by the previous lemma. Hence, we have $X = \tilde{X}$. $\Box$

$\textbf{Theorem 1.8.}$ Let $z_1,z_2,z_3$ be distinct and $w_1,w_2,w_3$ be distinct. Then there exists a unique $\l\in\Mob$ such that $\l(z_i) = w_i$.

$\textit{Proof.}$ Uniqueness is already given by the previous corollary. To show existence, we will give without loss of generality a $\l$ which sends $z_1$ to 1, $z_2$ to 0 and $z_3$ to $\infty$. This is because we can choose $\l$ such that $\l(z_i)=1,0,\infty$ and $\tilde{l}(w_i)=1,0,\infty$ such that $(\tilde{l}^{-1}\circ\l)(z_i)=w_i$ is a Möbius transformation. We give formulas for $\l$ by cases.

• Case 1: $z_1,z_2,z_3 \in \C$. Consider $\l(z) = \lr{\frac{z_1-z_3}{z_1-z_2}}\lr{\frac{z-z_2}{z-z_3}}.$
• Case 2: $z_1=\infty$. Consider $\l(z) = \frac{z-z_2}{z-z_3}.$
• Case 3: $z_2=\infty$. Consider $\l(z) = \frac{z_1-z_3}{z-z_3}.$
• Case 4: $z_3=\infty$. Consider $\l(z) = \frac{z-z_2}{z_1-z_2}.$ $\Box$

Notice that the image of a circle $C$ under the reciprocal map $z \mapsto \frac 1z$ is a circle unless $0 \in C$. Let us generalise this concept. A generalised circle in $\hC$ is a subset $C \subset \hC$ which is either a circle of a line $\cup\set{\infty}$. Then the following theorem tells us that Möbius transformations take circles or lines to circles or lines.

$\textbf{Theorem 1.9.}$ Let $\l \in \Mob$ and $C$ be a generalised circle. Then $\l(C)$ is a generalised circle.

$\textit{Proof.}$ Exercise by noticing that every Möbius transformation is a composite of $(z\mapsto az+b)$ and $(z\mapsto \frac 1z)$, and a line is the solution to the equation $Az + \bar{A}\bar{z} + c = 0$ for $A \in \C\setminus\set{0}, c \in \R$ and a circle is the solution to the equation $|z|^2 + Az + \bar{A}\bar{z} + c = 0$ for $A \in \C, c \in \R, c < |A|^2$. $\Box$

$\textbf{Theorem 1.10.}$ Let $z_1,z_2,z_3\in\hC$ be distinct points. Then there exists a unique generalised circle containing the $z_i$.

$\textit{Proof.}$ Existence: choose $\l$ such that $\l(1)=z_1,\l(-i)=z_2,\l(i)=z_3$. Then $\l(\text{unit circle})$ is a generalised circle containing $z_i$. Uniqueness: If $C$ and $C'$ are two circles containing $z_i$, choose $\l\in\Mob,$ $\l(z_i)=1,0,\infty$. Then $\l(C)$ and $\l(C')$ are generalised circles contianing $1,0,\infty$. i.e. $\l(C)$ and $\l(C')$ are lines containing 1, 0 such that $\l(C)=\l(C')$. Apply $\l^{-1}$ to get $C=C'$. $\Box$

We can understand a lot about holomorphic functions by looking at their line integrals.

For $f:D \in \C$ continuous, $D$ a domain, $\g:[a,b]\to D$ a piecewise $C^1$ (differentiable and continuous derivative) path, we can define a line integral by the chain rule

Some facts about line integrals that you think should hold do indeed hold. Their proofs are exercises for you.

1. Linearity. $\int_\g \a f+\b g\;dz$ = $\a\int_\g f\;dz$ $+$ $\b\int_\g g\;dz$ for $\a,\b\in\C$.
2. Invariance under speed of path. Let $\psi:[a,b] \to [a,b]$ piecewise $C^1$ with $\psi(a)=a,\psi(b)=b$. Then $\int_g f\;dz = \int_{\g\circ\psi} f\; dz.$
3. Opposite sign for swapping direction. Let $\psi:[a,b] \to [a,b]$ piecewise $C^1$ with $\psi(a)=b,\psi(b)=a$. Then $\int_g f\;dz = -\int_{\g\circ\psi} f\; dz.$

The length of $\g:[a,b] \to \C$ is $|g| := \int_a^b|g'(t)| dt$. We have a way to calculate an upper bound of a line integral as follows.

$\textbf{Lemma 2.1.}$ (ML-estimate) Let $f \in C(D)$, $\g$ a piecewise $C^1$ path in $D$, and suppose $|f(g(t))| \leq M$ for all $t \in [a,b]$. Then $|\int_\g f\;dz| \leq M\cdot|\g|$. With this we can say $|\int_\g f\;dz| \leq |\g| \sup_{z \in \g(t)} f(z)$.

$\textit{Proof.}$ We work straight from definitions.

Caution: you should never say the following as it does not make sense in the context of line integrals: $|\int_\g f\;dz| \leq \int_\g |f| dz$.

Let us provide some notation for paths which will be useful for later sections.

• Let $[z_1,z_2]$ denote linear interpolation with $[0,1]\to\C,$ $t\mapsto (1-t)z_1 + tz_2$.
• Let $\g^-$ denote the inverse of a path by $\g^-(t)=\g(b+a-t)$.
• Let $\g_n$ denote loops around the unit circle defined by $\g_n:[0,n]\to\C,$ $g_n(t) = e^{2\pi i t}$.
• Let $\cdot$ denote path composition, where $f \cdot g$ means we do the path $f$ first then $g$ in contrast with the order of function composition.
• Say a path is closed if its endpoints are the same.

$\textbf{Lemma 2.2.}$ Let $f \in C(D)$. Then the following are equivalent.

1. $\int_\g f(z) dz = \int_\tilde{\g} f(z) dz$ whenever $\g$ and $\tilde{\g}$ share the same endpoints.
2. $\int_\g f(z) dz = 0$ whenever $\g$ is closed.

$\textit{Proof.}$ Exercise. $\Box$

If $f\in C(D)$ and $F \in H(D)$ with $F'=f$, then $F$ is called a primitive of $f$ (on $D$). We want to know which continuous or holomorphic functions have a primitive. In this section we will show a very potent result that all holomorphic functions on a disk have a primitive. On the other hand, an example of a function that does not have a primitive is $\frac 1z$ on $\C \setminus\set{0}$ as we will show with the following proposition. The proof is application of the chain rule followed by the fundamental theorem of calculus for real variables.

$\textbf{Proposition 2.3.}$ Let $f\in C(D),$ $F\in H(D),$ $F' = f,$ $\g:[a,b]\to D$ a piecewise $C^1$ path. Then

$\textbf{Corollary 2.4.}$ If $f$ has a primitive on $D$, $\g$ and $\tilde{\g}$ are two paths in $D$ sharing same endpoints, then

The contrapositive of this results says that if the line integral yields different results for different paths with same endpoints, then $f$ does not have a primitive. Since $\int_{\g_n} \frac {1}{z} dz = 2\pi i n$, this means that $\frac 1 z$ does not have a primitive on $\C \setminus \set{0}$. Let us now build up the theory for the main result of this section.

$\textbf{Proposition 2.5.}$ Let $f \in C(\D(a,r))$ and suppose $\int_{\p T} f(z)dz=0$ for all triangles $T\subset\D(a,r)$. Then $f$ has a primitive on $\D(a,r)$.

$\textit{Proof.}$ Define $F:\Delta(a,r) \to \C$ by $F(z) = \int_{[a,z]} f\;dz$. We will show that $F$ is the primitive of $f$ with $F'=f$. Then

Now since $f$ is continuous we can find for a given $\e>0$ a small enough $\d$ such that for $|\D z| < \d$ we have $|f(z) - f(z_0)| < \e$. Then noting that $f(z_0)=\frac{1}{\D z}\int_{[z_0,z_0+\D z]} f(z_0)dz$ and recalling the ML-estimate, we have

Letting $\D z$ go to zero, we have $\frac{F(z_0 + \D z) - F(z_0)}{\D z} \to f(z_0)$. Hence, $F' = f$. $\Box$

Let us now provide the final piece of the puzzle with proof that is a bit more involved than any so far. Fun fact: this is the first major result that changed the history of complex analysis. Specifically, holomorphic functions used to be defined with the extra requirement that its derivative be continuous, but the following lemma leads to a string of results which show that this extra condition is redundant.

$\textbf{Lemma 2.6.}$ (Goursat's Lemma) Let $f \in H(\D(a,r))$. Then $\int_{\p T} f(z) dz = 0$ for all triangles $ \subset \Delta(a,r)$.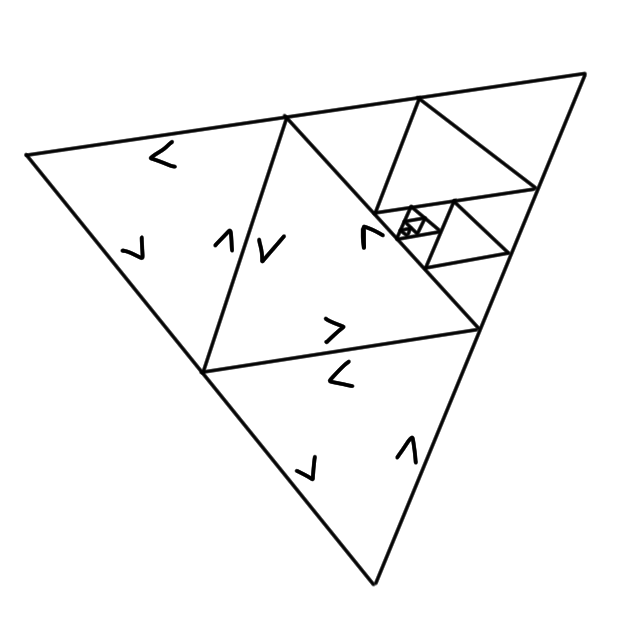

$\textit{Proof.}$ Bisect each side of $T$ to obtain four similar triangles scaled by $\frac 12$, $T',T'',T''',T''''$. Let

\begin{align} M &= \abs{\int_{\p T} f(z) dz} \\&= \abs{\int_{\p T'} f +\int_{\p T''} f +\int_{\p T'''} f +\int_{\p T''''} f}. \end{align}

The reason we do not get any other terms is because the middle sides occur twice but in opposite directions so they cancel out. By triangle inequality, at least one of $T',T'',T''',T''''$ has $\abs{\int_{\p T^?} f} \geq \frac M4$. Let $T^1$ be such a triangle and repeat this procedure to get a sequence of triangles $T=T_0\supset T_1\supset T_2\supset\ldots$ These triangles satisfy

1. $|\p T_n| = \frac{|\p T_0|}{2^n}$,
2. $\diam(T_n) = \frac{\diam(T_0)}{2^n}$, where $\diam(S):= \max_{z,w\in S} |z-w|$
3. $\abs{\int_{\p T_n} f(z) dz)} \geq \frac{M}{4^n}$.

Then I claim that $\bigcap_{n\geq 0} T_n = \set{z_0}$. For existence, we choose $w_j \in T_j$ for all $j$ and show that the sequence $w_j$ is Cauchy. Given $\e > 0$ we can find $N$ such that $n\geq N$ implies $\diam(T_n) < \e$. Then if $n,m \geq N$, we have $\abs{w_n,w_m}<\e$. Thus the sequence is Cauchy and $w_j \to z_0$ for some $z_0$. For each $n$, $w_m \in T_n$ for $m\geq n$ such that $z_0 \in T_n$ and $z_0 \in \bigcap_{n\geq 0} T_n$. For existence, suppose $z_0,z_0' \in \bigcap T_n$, but by above $z_0,z_0',z_0,z_0',\ldots$ is Cauchy so $z_0=z_0'$.

Write $f(z) = f(z_0) + f'(z_0)(z - z_0) + \a(z)(z - z_0)$ with

\begin{align} \a(z) = \begin{cases} \frac{f(z)-f(z_0)}{z-z_0} - f'(z_0) & z\not=z_0 \\ 0 & z=z_0. \end{cases} \end{align}

Since $f$ is $\C$-differentiable at $z_0$, $\a$ is continuous. With this, let us proceed to show that $M$ is zero

\begin{align} \frac {M}{4^n} &\leq \abs{\int_{\p T_n} f(z) dz} \\ &= \abs{\int_{\p T_n} f(z_0) + f'(z_0)(z-z_0) dz + \int_{\p T_n} \a(z) (z-z_0) dz} \\ &= \abs{\int_{\p T_n} \a(z) (z-z_0) dz} \\ &\leq |\p T_n| \cdot \max_{z \in \p T_n} |\a(z)| \cdot \max_{z \in \p T_n} |z - z_0| \tag*{by ML-estimate}\\ & \leq \lr{\frac {\p T_0}{2}} \lr{\max_{z \in \p T_n} |\a(z)|} \lr{\frac {\diam(T_0)}{2^n}} \\ &= |\p T_0| \diam(T_0) \cdot \frac {1}{4^n} \cdot \max_{z \in \p T_n} |\a(z)|. \end{align}

Because $\a(z_0)=0$ is continuous, we can choose $\d$ such that $|z-z_0| < \d$ gives us $|\a(z)| < \frac{\e}{|\p T_0|\diam(T_0)}$. So choosing $N$ big enough such that $\diam(T_n) = \max_{z \in \p T_n} |z-z_0|<\d$, we have

\begin{align} M \leq \max_{z \in \p T_n}|\a(z)| \to \e. \end{align}

This gives us $M=0$ so we are done. $\Box$

By a combination of the previous proposition and lemma, we have our desired results.

$\textbf{Corollary 2.7.}$ If $f \in H(\D(a,r))$, then $f$ has a primitive.

$\textbf{Corollary 2.8.}$ If $f \in H(\D(a,r))$, and $\g$ is a closed path in $\D(a,r)$, then $\int_\g f(z) dz = 0$.

In this section, we will show that line integration is invariant under homotopic paths under nice conditions. A powerful consequence of this is that a function holomorphic on any simply connected domain has a primitive, a generalisation of the focus of the previous section. We will recall the definition of homotopy from algebraic topology with a few differences and variants.

Let $\g,\tilde{\g}:[0,1] \to \C$ be paths. A homotopy from $\g$ to $\tilde{\g}$ is a continuous $\G:[0,1]\times[0,1]\to\C$ such that $\G(t,0) = \g(t)$ and $\G(t,1) = \tilde{\g}(t)$. Say $\G$ is a PCE-homotopy if for all $s$ $\G(0,s) = \g(0) = \tilde{\g}(0)$ and $\G(1,s) = \g(1) = \tilde{\g}(1)$. A CP-homotopy is a homotopy where $\G(0,s) = \G(1,s)$ for all $s$. If $\G([0,1]\times[0,1])\subset D$, say $\G$ is a homotopy in $D$ and that $\g$ and $\tilde{\g}$ are homotopic in $D$. It is probably easier to understand the definitions by just looking at a diagram.

$\textbf{Theorem 2.9.}$ (Homotopy independence of $\int$) Let $f \in H(D)$ and $\g$ and $\tilde{\g}$ be piecewise $C^1$ paths in $D$, $\G$ a homotopy $\g$ to $\tilde{\g}$. Suppose $\g^i = \G(0,s)$ and $\g^f = \G(1,s)$ are also piecewise $C^1$. Then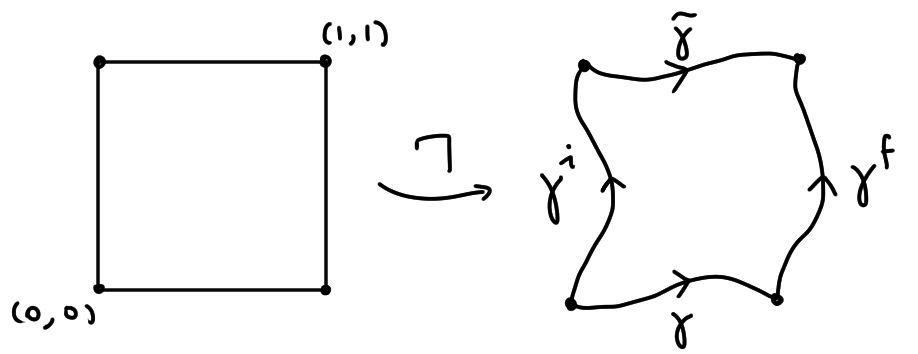

$$\int_\g f\;dz + \int_{\g^f} f\;dz = \int_{\g^i} f\;dz + \int_{\tilde{g}} f\;dz.$$

Furthermore, if $\G$ is a PCE or CP-homotopy, then

$$\int_\g f\;dz = \int_\tilde{g} f\;dz.$$

$\textit{Proof.}$ The main idea of the proof is that we can split $\G([0,1]\times[0,1])$ into small pieces and use the fact that the integral of a function holomorphic on a disk along closed paths is zero. The proof will spell this out in detail by using the following analysis fact and then showing that $\int_{\g\cdot\g^f\cdot\tilde{\g}^-\cdot{\g^i}^-} f\;dz = 0.$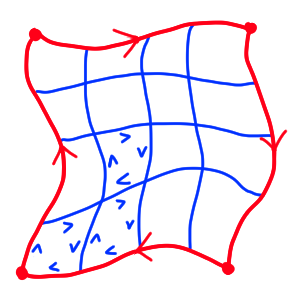

Let us quickly prove the analysis fact. Let $K \subset U \subseteq \C$ with $K$ compact and $U$ open. Then there eixts some $\e > 0$ such that for all $z \in K$, $\D(z,\e) \subset U$. To prove this, let $C = U^C$ and suppose there does not exist such an $\e$. Then there exists some $z_n \in K$ with $w_n \in C$ such that $|z_n-w_n| < \frac 1n$. Passing to a subsequence, assume $z_n \to z_0 \in K$. Then $w_n \to z_0$ as well. Since $C$ is closed, $z_0 \in C$. So $z_0 \in C \cap K$ which is a contradiction since $K \subset U$.

Then we have

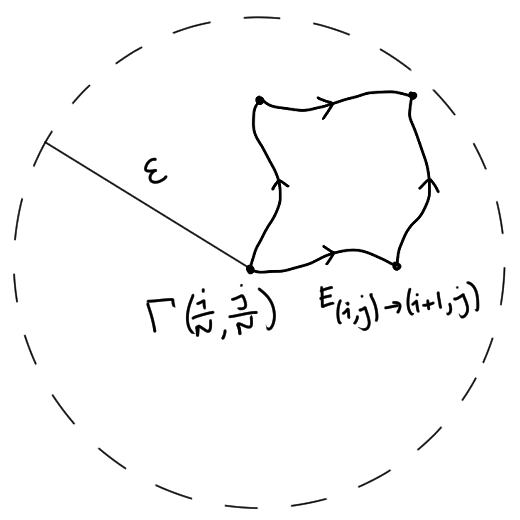
We now proceed to show for some $N$ that $\int_{\p S_{ij}} f(z)\;dz=0$ for all $i,j$. Observe that $\G([0,1]\times[0,1])$ is compact in $D$ which is open. By the analysis fact, choose $\e>0$ such that $\D(\G(s,t),\e) \subset D$ for all $s,t$. Since $[0,1]\times[0,1]$ is compact, $\G$ is uniformly continuous so choose $\d > 0$ such that $|s-s'|,|t - t'| < \d$ implies $|G(s,t) - G(s',t')| < \e.$ Choose $N$ such that $\frac 1n < \d$.

Now $z$ in the image of $\p S_{ij}$ is of the form $\G(s,t)$ with $|s - \frac iN| < \d$ and $|t - \frac jN| < \d$. Thus, $|\G(s,t) - \G(\frac iN, \frac jN)| < \e.$ So $\p S_{ij} \subset \D(\G(\frac iN, \frac jN), \e)$. Since $\p S_{ij}$ is closed and contained in a disk, we have $\int_{\p S_{ij}} f(z)dz = 0$. Thus, $\int_{\g\cdot\g^f\cdot\tilde{\g}^-\cdot{\g^i}^-} f\;dz=0$. $\Box$

One application of this is to show that path integrals of loops on simply connected domains are trivial. Recall that a domain $D \subset \C$ is called simply connected if every closed path is CP-homotopic to each other. Even more generally, if a loop is null homotopic, its path integral is trivial.

$\textbf{Corollary 2.10.}$ If $D$ is simply connected and $f \in H(D)$, then $\int_\g f(z) dz = 0$ for any closed path $\g$ in $D$. Hence $f$ has a primitive.

Before we end this section, we will state a helpful topology theorem without proof for showing that a domain is simply connected. Note that we can use the contrapositive of the corollary to show that a domain is not simply connected.

$\textbf{Theorem 2.11.}$ The following are equivalent for a domain $D \subseteq \C$

1. $D$ is simply connected
2. $\hC \setminus D$ is connected
3. $\p D$ in $\hC$ is connected

4. $\C \setminus D$ is connected
5. $\p D$ in $\C$ is connected.

The homotopy independence of integrals we proved in the previous section leads to the next interesting complex analysis result. Specifically, the value of a function $f$ on a circle determines its value everywhere inside a disk. This section will focus on spelling out this idea in detail. Firstly, we define what it means to be holomorphic on a closure on a domain. If $D$ is a domain, define

Here $\overline{D}$ denotes the closure of a domain $D$. Next, let $\p \D(a,r)$ denote the path $t \mapsto a + re^{2\pi i t}$ which goes around the disk centered at $a$ of radius $r$. Now we will state the theorem.

$\textbf{Theorem 2.12.}$ (Cauchy Integral Formula for disks) Let $f \in H(\overline{\D(a,r)}).$ Then for all $z \in \D(a,r)$,

$\textit{Proof.}$ Let

Then for all small $\e$, we have $I(\e) = \frac{1}{2\pi i} \int_{\p \D(a,r)} \frac{f(\z)}{\z-z} d\z$ since $\p \D(a,r)$ and $\p \D(z,\e)$ are CP-homotopic in $\D(a,r) \setminus \set{z}$ by linear interpolation. Thus, we will show that $\lim_{\e \to 0} I(\e) = f(z)$.

Observe that $\frac 1{2\pi i} \int_{\p \D(a,r)} \frac 1{\z - a} d\z = 1$ for any $r$. This can be shown by direct integration or noticing that it is some shift and homotopy of $\int_{\text{circle}} \frac 1z$. Thus, we have

Then we have

A few details for the last line: since $\z \in \D(z,\e)$, we have $\abs{\z-z} = \e$. Moreover, we can take the limit $\e \to 0$ since $f$ is holomorphic and hence continuous. $\Box$

As mentioned briefly above, the Cauchy integral formula means that a function $f \in H(\overline{D})$ is determined solely by values on its boundary.

$\textbf{Corollary 2.13.}$ If $f,g \in H(\overline{\D(a,r)})$ and $f(z) = g(z)$ for $z \in \p\D(a,r)$, then $f=g$.

We will now use the Cauchy integral formula to show that a function holomorphic on an arbitrary domain is infinitely many times $\C$-differentiable. This makes the old definition of holomorphic redundant, specifically how the derivative of a holomorphic function has to be continuous. We begin with the following proposition with proof given by a very typical analysis argument.

$\textbf{Proposition 2.14.}$ Let $g \in C(\p\D(a,r)).$ Define

for $z \in \D(a,r)$. Then $f$ is infinitely many time differentiable with

$\textit{Proof.}$ First we will prove the following seemingly arbitrary fact. Let $k>0$ be an integer. Then there exists a polynomial $p(a,b)$ such that for all $a,b\in\C, a\not=b, a\not=0$,

The proof of this claim is purely algebraic with the idea that we let $(a-b)^k = a^k - kba^{k-1} + b^2q(a,b)$. The main point of this claim as we will see later is that we have a factor of $b^2$ on the right hand side.

We will prove the proposition by induction on $k$. For $k=0$, the result follows by definition of $f$. Now assume true for $k=0$. Then we have

Now for a few notes for the final line. Firstly recall that the $2\pi r$ term comes from the length of the path by the ML-estimate. Secondly, observe that the $\sup$ term is bounded above and independent of $\D z$ for $|\D z| < \frac 12 |z-z_0|$. So letting $\D z$ go to 0, we have the above term go to zero. By definition of complex differentiable this gives us the desired result. $\Box$

$\textbf{Corollary 2.15.}$ If $f\in H(D)$, $f' \in H(D)$. So $f$ is infinitely many times $\C$-differentiable.

$\textit{Proof.}$ We will use the fact that differentiability is a local property. Specifically, I claim that $g:D \to \C$ is holomorphic if and only if for all $z_0 \in D$, there is some $r>0$ such that $g \mid_{\D(z_0,r)} \in H(\D(z_0,r))$. Given $z_0 \in D$, choose $r > 0$ such that $\overline{\D(z_0,r)} \subset D$. Now by the Cauchy integral formula on $\D(z_0,r)$, we have $f(z) = \frac 1{2\pi i} \int_{\p\D(z_0,r)} \frac{f(\z)}{\z-z} d\z$. By the previous proposition, $f'\mid_{\D(z_0,r)} \in H(\D(z_0,r))$. In particular, $f'$ is $\C$-differentiable at $z_0$. Since $z_0$ was arbitrary, $f' \in H(D)$. $\Box$

$\textbf{Corollary 2.16.}$ $f'$ is continuous on $D$.

In this section we generalise the Cauchy integral formula to a bigger class of domains known as Jordan domains. Geometrically, these look like simply connected domains with smaller simply connected domains cut out of them where its boundary does not cross over itself. However, this definition is very vague so we will proceed to define Jordan domains more rigorously.

A Jordan path is a closed simple path $\g:[0,1] \in \C$. A simple path is such that $\g(a) \not = \g(b)$ unless $a=b$ or $a=0,b=1$ or $a=1,b=0$. This means that a Jordan path has no self intersections. A Jordan curve $\G \subset \C$ is a curve such that $\G = \g([0,1])$ for some Jordan path $\g$, called Jordan parametrisation of $\G$. A Jordan arc is the image of an injective $\g:[0,1] \to \C$. This is like a Jordan path but not a loop. Note that this last definition is only used for the proof of the following lemma which states that a path integral is invariant under Jordan parametrisation up to orientation.

$\textbf{Lemma 2.17.}$ Let $\G$ be a Jordan arc or curve and let $\g$ and $\tilde{\g}$ be two Jordan parametrisations of $\G$. Then for all $f$ holomorphic in an open neighbourhood of $\G$ either

$\textit{Proof.}$ We will prove for Jordan arcs as the result for Jordan curves comes from noticing that a curve is the composite of two arcs. Suppose $\g([0,1]) = \tilde{\g}([0,1]) = \G$ bijective. Then either $\g(0)=\tilde{\g}(0)$ and $\g(1)=\tilde{\g}(1)$ or $\g(0)=\tilde{\g}(1)$ and $\g(1)=\tilde{\g}(0)$. Recall that because $[0,1]$ is compact, $\g^{-1}$ is continuous. Define a PCE-homotopy from $\g$ to $\tilde{\g}$ by $\L(s,t) = \g(st + (1-s)\g^{-1}(\tilde{\g}(t))).$ By homotopy independence of integrals, this gives us the first equation. For the second case, reverse a curve and apply the same homotopy to get the second equation. $\qed$

The upshot of this is that if $\G$ is an oriented Jordan curve, then $\int_\G f(z) dz$ is well defined by integrating any Jordan parametrisation if $h$ is holomorphic in a domain containing $\G.$ Thus, we notate $\int_\G f(z) dz$ to mean $\int_\g f(z) dz$ for any $\g$ a Jordan path with the correct orientation.

Then define a Jordan domain to be a domain $D$ whose boundary if a finite collection of disjoint Jordan curves $\set{\G_j}.$ The standard orientation is to have the domain on the left of a path. Then have we have notation $\int_{\p D} f(z) dz = \sum_j \int_{\G_j} f(z) dz$ for $f \in H(\overline{D})$ with respect to the standard orientation. There are two possible proofs for the following theorem, one intuitive geoemtric version and one purely algebraic using Green's theorem. We will omit the latter and refer you to Wikipedia for it.

$\textbf{Theorem 2.18.}$ (Cauchy Integral Theorem) Let $D$ be a bounded Jordan domain, $f \in H(\overline{D}).$ Then $\int_{\p D} f(z) dz = 0.$

$\textit{Proof by picture.}$ We homotope an extended boundary to a point.

We now end this section and chapter with the Cauchy integral formula for bounded Jordan domains. There's actually a formula for certain unbounded Jordan domains, I'll let you think about what other assumptions we might need and what the resulting formula is.

$\textbf{Theorem 2.19.}$ (Cauchy Integral Formula for Jordan domains) Let $D$ be a bounded Jordan domain and $f \in H(\overline{D}).$ Then for $k=0,1,2,\ldots$

$\textit{Proof.}$ We will provide a picture and an equation and let you fill out the details. Let $\tilde{D} = D \setminus \overline{\D(z,e)}.$

In this section we will get a correspondence between holomorphic functions and power series which does not occur in real analysis.

You might be familiar with pointwise and uniform convergence of functions. We will define a type of convergence that is stronger than pointwise but weaker than uniform which will give us very nice results in complex analysis. Nevertheless, we will begin by recalling some definitions for completeness.

Let $S \subset \C$, $f:S\to \C$. A sequence $f_n:S \to \C$ converges pointwise to $f$ if for all $z \in S$, $f_n(z) \to f(z).$ A sequence $f_n$ converges uniformly to $f$ if all every $\e>0$, there exists $n \in N$ such that $n\geq N$ implies $|f_n(z) - f(z)| < \e$ for all $z \in S.$ Also recall that uniform convergence preserves integration but not differentiability in real analysis.

We will introduce a new type of convergence now with two equivalent definitions and show that it preserves path integration, continuity and even differentiation. Let $U \subset C$ be open, $f_n,f: U \to \C.$ Say $f_n \to f$ normally on $U$ if one (and hence the other) of the following holds

1. For all $z \in U,$ there exists open $V \subset U$ with $z \in V$ such that $f_n \to f$ uniformally on $V.$
2. For all compact $K \subset U,$ $f_n \to f$ uniformly on $K.$

$\textit{Proof of equivalent definitions.}$ $(1. \implies 2.)$ Let $K \subset U$ be compact. Choose for each $z \in K$ an open $V_z \in U$ such that $z \in V_z$ and $f_n \to f$ uniformally on $V_z.$ Note that $K \subset \bigcup_{z\in K} V_z.$ Let $w_1,\ldots,w_m$ be a finite subcover of $K$ by compactness and $V_z.$ Then $f_n \to f$ uniformally on $W_1\cup\ldots\cup W_m$ such that $f_n \to f$ uniformally on $K.$

$(2. \implies 1.)$ Let $z \in U.$ There exists some $\e>0$ such that $\D(z,\e) \subset U.$ Then $\overline{\D(z,\e/2)} \subset U$ by compactnes in $\C$ such that $f_n \to f$ uniformally on $\overline{\D(z,\e/2)}.$ So $f_n \to f$ uniformally on $\D(z,\e).$ $\qed$

$\textbf{Proposition 3.1.}$ Let $f,f_n \in C(D),$ $\g$ is a piecewise $C^1$ path in $D$, and suppose $f_n \to f$ normally on $D$. Then

$\textit{Proof.}$ We use the second definition of normal convergence.

Since $\im(\g)$ is compact, $f_n \to f$ uniformally on $\im(\g)$ so $\sup_{z\in\im(\g)}\abs{f_n(z)-f(z)}\to 0.$ $\qed$

$\textbf{Proposition 3.2.}$ Let $f_n,f: U \to \C,$ $f_n \in C(U),$ $f_n\to f$ normally on $U.$ Then $f \in C(U).$

$\textit{Proof.}$ Let $z \in U.$ Take $z \in V_z \subset U$ such that $f_n \to f$ uniformally on $V_z.$ So $f\mid_{V_z}$ is continuous by real analysis. Thus, $f$ is continuous at $z$ and since $z$ was arbitrary, $f \in C(U).$ $\qed$

$\textbf{Theorem 3.3.}$ Let $f_n\in H(D),$ $f_n\to f$ normally. Then $f \in H(D),$ and $f_n^{(k)} \to f^{(k)}$ normally on $D.$

$\textit{Proof.}$ Since holomorphic is a local property it is a good idea to use the first definition of normal convergence. Fix $a \in D$ and pick $\e>0$ such that $\D(a,2\e) \subset D$ and hence $\overline{\D(a,\e)} \subset D.$ Now I claim that $f_n^{(k)}(z) \to \frac{k!}{2\pi i}\int_{\p \D(a,\e)} \frac{f(\z)}{(\z-z)^{k+1}} dz$ uniformally on $\D(a,\e/2).$ By the Cauchy integral formula for disks, we have

Note by geometry that for $z \in \D(a,\e/2),$ we haev $\abs{\z - z} \geq \e/2$ for $\z \in \p\D(a,\e)$. So the distance between $\z$ and $\z$ is not arbitrarily small and we have $\abs{\frac{1}{(\z-z)^{k+1}}} \leq \lr{\frac{z}{\e}}^{k+1}.$ So continuing from above, we have by the ML-estimate normal convergence

In particular, $f_n(z) \to f(z)$ such that $f(z) = \frac{1}{2\pi i} \int_{\p\D(a,\e) \frac{f(\z)}{\z - z} dz}.$ Since $f \in C(\overline{\D(a,\e)})$ this function is holomorphic on $\D(a,\e/2)$ so in particular, $f$ is $\C$-differentiable at $a$. Given that $a$ was arbitrary, $f \in H(D).$ So now $f_n^{(k)}(z) \to \frac{k!}{2\pi i} \int_{\p\D(a,\e)} \frac{f(\z)}{(\z-z)^{k+1}} dz = f^{(k)}(z)$ uniformally on $\D(a,\e/2).$ So $f_n^{(k)} \to f^{(k)}$ normally. $\qed$

In this section we show what the title suggests. This is a very interesting result to even more interesting facts. Note that although one direction holds for real analysis, the converse is not true. We begin with some more definitions and basic proprositions.

If $z_n$ is a sequence in $\C$, then say $\sum_{k=1}^n z_k$ converges absolutely if $\sum_{k=1}^\infty |z_k| < \infty.$ This is true also in real analysis. We will also state some real analysis absolute convergence facts extended to the complex field and skip their proofs.

$\textbf{Theorem 3.4.}$

1. If $\infsum{k=1}z_k$ converges absolutely, then any rearrangement converges to the same value.
2. If $\infsum{n,k=1}|z_{n,k}| < \infty,$ then $\infsum{n=1}\lr{\infsum{k=1}z_{n,k}} = \infsum{k=1}\lr{\infsum{n=1}z_{n,k}}.$
3. If $\infsum{n=1}z_n$ and $\infsum{k=1}w_k$ converge absolutely, $\lr{\infsum{n=1}z_n}\lr{\infsum{k=1}w_k} = \infsum{n,k=1} z_n w_k.$

$\textbf{Lemma 3.5.}$ (M-test for numbers) If $z_k \in \C$ and $a_k \in \R_{\geq 0}$ with $|z_k| \leq a_k$ for all $k$ and $\infsum{k=1} a_k < \infty,$ then $\infsum{k=1} z_k$ converges (absolutely).

$\textbf{Lemma 3.6.}$ (M-test) Let $f_k : S \to \C$ and suppose there exists $a_k$ such that $|f_k(z)| \leq a_k$ for all $z \in S,$ and $\infsum{k=1} a_k < \infty.$ Then $\infsum{k=1} f_k$ converges uniformally and absolutely to a function $f:S \to \C.$

$\textbf{Proposition 3.7.}$ (Abel's theorem) If $\infsum{k=0} c_k(z-a)^k$ converges at $z=z_0,$ then it converges normally and absolutely on $\D(a,|a-z_0|).$

$\textbf{Corollary 3.8.}$ If $\infsum{n=0}c_n(z-a)^n$ is a power series, there is a number $R \in [0,\infty]$ such that it

• converges normally and absolutely on $\D(a,R)$
• diverges if $|z-a| > R$

Here $R$ is the radius of convergence and $\D(a,R)$ is the disk of convergence. Also let $\D(a,\infty) = \C$. The following theorem gives a way to calculate $R$ but first we need to introduce a new definition. If $a_n$ is a sequence of real numbers, then $\limsup a_n$ exists and is defined by

Note that $\sup_{k \geq n} a_k$ is always decreasing and the $\limsup$ always exists in $[-\infty,\infty].$ Moreover, if $a_n$ converges, then we have $\limsup a_n = \lim a_n.$

$\textbf{Theorem 3.9.}$ The radius of convergence of $\infsum{n=0} c_n(z-a)^n$ is $\lr{\limsup_{n\to\infty} |c_n|^\frac{1}{n}}^{-1}.$

With this previous theorem, we get that a power series always converges normally to a holomorphic function on some disk. However, this is also true in real analysis. From this point we show that a holomorphic function on a disk is associated with a power series, and this fact is not true in real analysis. Let us recall Taylor series for holomorphic functions. If $f \in H(\D(a,r))$ or more generally $f \in H(D)$ with $a \in D,$ the Taylor series of $f$ centered at $a$ is

We now prove the main result for this section by starting with a lemma.

$\textbf{Lemma 3.10.}$ If $f \in H(\D(a,r))$ and $f(z) = \infsum{n=0} c_n(z-a)^n$ for all $z \in \D(a,r)$ then $c_n = \frac{f^{(n)}}{n!}.$

$\textit{Proof.}$ Since the series converges, $r \leq R,$ and the partial sums converge normally to $f$, then $f^{(k)}(z)$ $=$ $\infsum{n=0} n(n-1)\ldots(n-k+1)c_n(z-a)^{n-k}.$ Evaluating at $z=a$ gives $f^{(k)}(a) = k!c_k$ by seeing that the only term that does not cancel is $n=k.$ $\qed$

$\textbf{Theorem 3.11.}$ Let $f \in H(\D(a,r)).$ Then there exists a unique power series $\infsum{n=0} c_n(z-a)^n$ which converges normally to $f$ on $\D(a,r)$ and it is the Taylor series.

$\textit{Proof.}$ Uniqueness and convergence to a Taylor series is given from the previous lemma (though we will show again explicitly that the convergent series is the Taylor series). For existence, let $0 < \r < r.$ Then $f \in H(\overline{\D(a,\r)})$. Begin with the case $a=0.$ If $z \in \D(a,\r)$ and $\z \in \p\D(0,\r)$ then $\frac{f(\z)}{\z-z} = \frac{f(\z)}{\z}\lr{\frac{1}{1-\frac{z}{\z}}}.$ On $|z| < |\z|$ we have normal convergence $\frac{f(\z)}{\z}\lr{\frac{1}{1-\frac{z}{\z}}} = \frac{f(\z)}{\z} \infsum{n=0} \frac{z^n}{\z^n}.$ Then by Cauchy's integral formula

Since $\r$ was arbirary, this holds for all $z \in \D(0,r).$ Now consider arbitrary $a$, $f \in H(\D(a,r)).$ Let $g(z) = f(z+a)$ so $g \in H(\D(0,r)).$ Then by the chain rule we have $f(z)$ $=$ $g(z-a)$ $=$ $\infsum{n=0} \frac{g^n(0)}{n!}(z-a)^n$ $=$ $\infsum{n=0} \frac{f^n(a)}{n!}(z-a)^n.$ $\qed$

One useful theorem given by this correspondence is that a holomorphic function is defined by a sequence convergent inside its domain. Another fact is that a bounded entire function is constant.

$\textbf{Theorem 3.12.}$ (Uniqueness/Identity theorem) Let $f,g \in H(D)$ for a domain $D.$ Suppose there exists a sequence $z_n \in D$ of distinct points such that $z_n$ converges in $D,$ and that $f(z_n) = g(z_n)$ for all $n.$ Then $f=g.$

$\textit{Proof.}$ Without loss of generality let $g=0$ and replace $f$ with $f-g.$ Let $S$ $=$ $\set{z\in D \mid f^{(n)}(z)=0}.$ We show that $S=D$ implies $f\equiv 0$ by showing that $S$ nonempty, open and closed by definition of connectedness.

• For nonempty, let $a = \lim_{k\to\infty} z_k \in D,$ where $f(z_k) = 0$ for all $k.$ We will show that $f^{(n)}(a) = 0$ such that $a \in S$ by contradiction. Let $n_0$ be the smallest nonnegative integer such that $f^{(n_0)}(a) \not=0.$ For some $r > 0,$ we have power series expansion on $\D(a,r)$
  \begin{align} f(z) &= \infsum{n=0} \frac{f^{(n)}(a)}{n!}(z-a)^n \\ &= \infsum{n=n_0} \frac{f^{(n)}(a)}{n!}(z-a)^n \\ &= (z-a)^{n_0} \infsum{n=n_0} \frac{f^{(n)}(a)}{n!}(z-a)^{n-n_0}. \end{align}

  So $p(z) = \infsum{n=n_0} \frac{f^{(n)}(a)}{n!}(z-a)^{n-n_0}$ converges on $\D(a,r)$ normally to a holomorphic function and $f(z) = (z-a)^{n_0} p9z)$ with $p(a) = \frac{f^{(n_0)}(a)}{n_0!} \not = 0.$ Since $z_k \to a,$ and the $z_k$ are distinct, there is some $z_{k_0} \in \D(a,r)$ with $z_{k_0} \not = a.$ Then $0 = f(z_{k_0}) = (z_{k_0} - a)^{n_0} p(z_{k_0}).$ Thus $p(z_{k_0}) = 0$ since $z_{k_0} \not =a.$ But this applies to all but finitely many $z_k$ and by continuity $p(a)$ $=$ $\lim_{k\to\infty} p(z_k)$ $=$ $\lim_{k\to\infty} 0 = 0.$ This contradicts $p(a) \not = 0.$

• For $S$ open, let $z_0 \in S.$ Then for some $r>0,$ $f(z)$ $=$ $\infsum{n=0} \frac{f^{(n)}(z_0)}{n!}(z-z_0)^n$ $= 0$ on $\D(z_0,r).$ So $\D(z_0,r) \subset S$ and hence $S$ open.
• For $S$ closed, we have $S = \bigcap_{n=0}^\infty {f^{(n)}}^{-1}\set{0}$ and $f^{(n)}$ is continuous such that its preimage is closed. $\qed$

$\textbf{Theorem 3.13.}$ (Liouville's Theorem) If $f$ is a bounded entire function, then it is constant.

$\textit{Proof.}$ Write $f(z) = \infsum{n=0} c_nz^n$ converging normally on $\C.$ We show $c_n=0$ if $n\geq 1.$ Fix $n\geq 1$ and suppose $r > 0$ so $f \in H(\overline{\D(0,r)}).$ Then we have $c_n =\frac 1{2\pi i} \int_{\p\D(0,r)} \frac{f(\z)}{\z^{n+1}} d\z.$ Choose $M$ such that $|f(z)| \leq M$ for all $z \in \C.$ Then by the ML-estimate $|c_n|$ $\leq$ $\frac 1{2\pi} \cdot 2 \pi r \cdot \sup_{|\z|=r} \frac{|f(\z)}{|\z|^{n+1}}$ $=$ $\frac 1{r^n} M \xrightarrow{r\to\infty} 0.$ So $f(z) = c_0$ for all $z.$ $\qed$

We try to generalise the above result to holomorphic functions on annuli which we will use to study "isolated singularities". This will let us study functions $f \in H(\D(a,r)\setminus\set{a})$ which will give us some important theorems concerning roots of functions.

Define

and let

Say it converges absolutely if both series converges absolutely. Note that this is stronger than $\lim_{N\to\infty} \sum_{n=-N}^N a_n$ converging. For example $a_n=n$ converges under this definition but not the former.

Then a Laurent series is one of the form $\sum_{n=-\infty}^\infty c_n(z-a)^n.$ Define for $0 \leq r_1 < r_2 \leq \infty$ an annulus

Note that a Laurent series converges normall on $\D(a,r_1,r_2)$ to a holomorphic function where $r_1$ is what makes $\sum_{n=1}^\infty c_n(z-a)^n$ converge for $|z-a|>r_1$ and $r_2$ is what makes $\sum_{n=0}^\infty c_n(z-a)^n$ converge for $|z-a| < r_2$ (exercise!). We'll now see that if $f \in H(\D(a,r_1,r_2))$ then there exists a unique Laurent expansion of $f$, giving us correspondence between holomorphic functions on annuli and Laurent series.

$\textbf{Theorem 3.14.}$ Let $f \in H(\D(a,r_1,r_2)).$ Then there exists a unique laurent series $\sum_{n=-\infty}^\infty c_n(z-a)^n$ converging normally and absolutely to $f$ on $\D(a,r_1,r_2).$ Moreover, for arbitrary $r_1 < \r < r_2$ we have

$\textit{Proof.}$ Without loss of generality, let $a=0$ by considering $g(z) = f(z+a) \in H(\D(0,r_1,r_2)).$ Let $r_1 < \r_1 < \r_2 < r_2$ such that $f \in H(\overline{\D(0,\r_1,\r_2)})$ and let $z \in \D(0,\r_1,\r_2).$ By the Cauchy integral formula, we have

Now we consider each integral sum component separately. Let $f_{in}(z)$ $=$ $\int_{|\z|=\r_2} \frac{f(\z)}{\z-z} d\z$ and $f_{out}(z)$ $=$ $\int_{|\z|=\r_1} \frac{f(\z)}{\z-z} d\z.$ For the first integral, we use the geometric series expansion of $\frac 1{1-\frac z\z}$ as follows

For the second sum, note that $|z| > |\z|$ so the geometric series expansion is a bit different

Thus, we have

So $f(z)$ $=$ $\frac{1}{2\pi i} \sum_{n=-\infty}^{\infty}z^n \lr{\int_{|\z|=\r_1} \frac{f(\z)}{\z^{n+1}} d\z}$ converges normally to $f$ on $\D(0,\r_1,\r_2).$ So $f$ converges normally on $\D(0,r_1,r_2)$ $=$ $\bigcup \D(0,\r_1,\r_2).$ $\qed$

If $f \in H(D)$ and $a \not\in D$ but $\D(a,0,r) \subset D$ for some $r>0,$ then $a$ is an isolated singularity of $f.$ First define the principal part of a Laurent expansion is $\sum_{n=-\infty}^{-1}c_n(z-a)^n.$ We can classify isolated singularities as follows and later we will give equivalent definitions. A singularity is

• removable if principal part is 0,
• a pole if principal part is finite (there exists a highest positive $N$ such that $c_{-N}\not=0$ and $c_{-M}=0$ for all $M > N$),
• essential if principal part is infinite.

$\textbf{Theorem 3.15.}$ The following are equivalent

1. $a$ is a removable singularity
2. $f$ has a holomorphic extension on $\D(a,r)$
3. $\lim_{z\to a} f(z)$ exists
4. $f(z)$ is bounded on $\D(a,0,r)$ for some $r.$

$\textit{Proof.}$ Firstly, for removable singularities. For $1 \implies 2,$ we have $f(z) = \sum_{n=0}^\infty c_n(z-a)^n$ on $\D(a,0,r).$ By Abel's theorem, this power series converges normally on $\D(a,r)$ to $g \in H(\D(a,r)).$ By construction $g\mid_{\D(a,0,r)} = f.$ Continuity gives us $2 \implies 3$ and $3 \implies 4.$

For $4 \implies 1,$ recall for any $0< \r < r$ we have $c_n$ $=$ $\frac 1{2\pi i} \int_{\p\D(a,\r)} \frac{f(\z)}{(\z-a)^{n+1}} d\z.$ Choose $\r < \e,$ and choose $M$ such that $|f(z)| \leq M$ on $\D(a,0,\e).$ By the ML estimate we have

If $n < 0,$ then $|c_n| \leq \lim_{\r \to 0} \frac M{\r^n} = 0.$ So the principal part of $f$ at $a$ is 0. The upshot of this is that if $f \in H(D)$ has an isolated singularity at $z=a$ and $f\mid_{\D(a,0,r)}$ is bounded for some $r,$ then $f$ extends to a $g \in H(\D \cup \set{a}),$ such that we "removed the singularity".

Now we look at poles. For the foward implication, write $f(z) = \sum_{n=-N}^\infty c_n(z-a)^n$ for $N>0.$ Then $f(z)$ $=$ $(z-a)^{-N}\sum_{n=-N}^\infty c_n(z-a)^{n+N}$ $=$ $(z-a)^{-N}\sum_{n=0}^\infty c_{n-N}(z-a)^n$ where this series on $\D(a,0,r),$ has removable singularity. Write $f(z)$ $=$ $\frac{p(z)}{(z-a)^N}$ with $p(a) \not=0,$ $p \in H(\D(a,r)).$ So $\lim_{z \to a} \frac{|p(z)|}{|z-a|^N} \to \infty.$

Now for the converse direction. choose $\D(a,0,\e)$ on which $|f(z)| \geq 4204.$ Then $\frac 1{f(z)} \in H(\D(a,0,\e))$ and $\lim_{z \to a}\frac 1{|f(z)|} = 0$ by assumption. So $\frac 1 f$ extends to a function $g$ holomorphic on $\D(a,r)$ with $g(a) = 0.$ Write on $\D(a,r)$

This sum converges normally to $p \in H(\D(a,r))$ with $p(a) \not=0.$ So $f(z)$ $=$ $\frac 1 {g(z)}$ $=$ $\frac{1}{(z-a)^N}\cdot \frac 1{p(z)}.$ Since $p(a) \not=0,$ $\frac 1{p(a)} \in H(\D(a,\r)).$ Write $\frac 1{p(a)}$ $=$ $\sum_{n=0}^\infty d_n(z-a)^n$ on $\D(a,\r).$ So $f(z)$ $=$ $\frac 1{(z-a)^N} \sum_{n=0}^\infty d_n(z-a)^{n-N}$ which has finite principal part. $\qed$

Now we see that roots and zeroes are closely related. Suppose $f \in H(D)$ with isolated singularity at $a$ (or $a \in D$) either a pole or removable and $f \not\equiv 0.$ Then we can write $f(z)$ $=$ $c_n(z-a)^N$ $+$ $c_{N+1}(z-a)^{N+1})$ $+\ldots$ with $c_N \not = 0.$ If $N \geq 0,$ $a$ is removable or $a \in D.$ If $N>0,$ then $a$ is a zero of order $N$, if $N < 0,$ then $a$ is a pole of order $-N.$ A simple pole is a pole with order $0.$ Likewise a simple zero is a zero with order $0.$

We have $f$ has a zero of order $N$ at $a$ if and only if $f(z) = (z-a)^Np(z)$ with $p(a) \not=0$ and $p$ holomorphic. Similarly, $f$ has a pole of order $N$ if and only if $f(z) = \frac{p(z)}{(z-a)^N}$ with $p(a) \not=0$ and $p$ holomorphic.

$\textbf{Theorem 3.16.}$ (Casorati-Weierstrass Theorem) Let $f \in H(\D(a,0,r))$ with an essential singularity at $z=a.$ Then for all $A \in \C \cup \set{\infty}$ there is a sequence $z_n \to a$ such that $f(z_n) \to A.$

$\textit{Proof.}$ First suppose $A=\infty.$ Since the singularity is not removable, $f\mid_{\D(a,0,\frac 1n)}$ is unbounded, so there exists $z_n \in \D(a,0,\frac 1n)$ such that $|f(z_n) \geq n.$ Then by construction $z_n \to a,$ $|f(z_n)| \to A =\infty.$

Let $A \in \C.$ Then $f(z) - A$ has an essential singularity at $z = 0,$ since only change $c_0.$ If there exists $z_n \to a,$ such that $f(z_n) = A$ for all $n$ and we are done. If there does not, $\frac 1{f(z)-A} \in H(\D(a,0,\d)).$ Since having a pole or removable singularity is preserved by reciprocal, $\frac 1{f(z) - A}$ has an essential singularity at $z=a.$ Choose $z_n \to a,$ $\frac 1{|f(z_n)-A|} \to \infty.$ Then $f(z_n) \to A.$ $\qed$

There is actually a stronger version of this theorem which we shall state, but its proof requires stuff out of the scope of this class.

$\textbf{Theorem 3.17.}$ (Great Picard) If $f$ has an essential singularity at $z=a,$ then $f(\D(a,0,\d)) = \C$ or $\C \setminus \set{w}$ for some $w.$

Before we conclude this section, we give a more general version of the Cauchy integral theorem with our definition of singularities, or more specifically poles. First, let $f \in H(D)$ and $a$ an isolated singularity. Then the residue of $f$ at $a$ for $\r$ such that $\D(a,0,\r) \subset D$

$\textbf{Theorem 3.18.}$ (Residue Theorem) Let $f$ $\in$ $H(\overline{D} \setminus\set{a_1,\ldots,a_n})$ for $a_j \in D$ a bounded Jordan domain. Then

$\textit{Proof.}$ Let $\tilde{D}$ $=$ $D$ $\setminus$ $(\overline{\D(a_1,\e_1)} \;\cup$ $\ldots$ $\cup\; \overline{\D(a_n,\e_n)})$ for $e_j$ small enough. Then $\int_{\p\tilde{D}} f(z) dz = 0$ by the Cauchy integral formula. Thus, we have

We now have all the machinery required to prove some of the big complex analysis theorems. The open mapping theorem states that holomorphic functions map open domains to open domains. This is not true in $\R$, for example $x^2$ maps $\R$ to $[0,\infty).$ The Riemann mapping theorem states that there is a conformal equivalence between every simply connected domain that is not $\C$ and the unit disk. We continue from residues.

We prove the open mapping theorem first by looking at relations between integrals and zeroes and poles of a function on a domain.

$\textbf{Theorem 4.1.}$ (Argument Principle version 1) Let $D \subset \C$ be a bounded Jordan domain and $f \in H(\overline{D} \setminus \set{a_1,\ldots,a_n})$ with poles $a_j.$ Let $b_1,\ldots,b_k$ be the zeroes of $f$ and assume $f$ has no zeroes on $\p D.$ Let $N_i$ be the order of $a_i$ and $K_j$ be the order of $b_j.$ Further, let $K = \sum K_j$ and $N = \sum N_i.$ Then

$\textit{Proof.}$ Note that $\frac{f'}{f}$ has isolated singularities at $a_1,\ldots,a_n,b_1,\ldots,b_k.$ Now we claim that if $g(z) = (z-a)^Rp(z)$ with $p(a) \not = 0$ arbitrary but $p$ holomorphic near $a$ we, then $\frac{g'}{g}$ has a simple pole with residue R at $a.$ To see this, we differentiate and get $\frac d{dz} (z-a)^Rp(z)$ $=$ $D(z-a)^{R-1}p(z)$ $+$ $(z-a)^Rp'(z).$ Hence, $\frac {g'(z)}{g(z)} = R(z-a)^{-1} + \frac{p'(z)}{p(z)}$ and since $\frac{p'(z)}{p(z)}$ is holomorphic near $a$, it expands as a power series, leaving $c_{-1} = R$ in the Laurent expansion of $\frac{g'}{g}.$

Note that $f$ has zeroes of order $K_j$ at $b_j$ and poles of order $N_j$ at $a_j$ and that $\frac{f'}{f}$ has simple poles at all of $a_1,\ldots,a_n,b_1,\ldots,b_k.$ By our claim we have $\res_{a_j}\frac{f'}{f} = -N_j$ since $f(z)$ $=$ $(z-a_j)^{-N_j}p(z)$ locally around $a_j.$ Similarly, $\res_{b_j} \frac{f'}{f} = K_j.$ Thus by the residue theorem, we have

Now we want a geometric version of this statement. We see that $\frac{f'}{f}$ looks like a derivative of $\ln(f(z))$ in the real sense and want to extend this idea to the complex setting. What we do know is that $\int_{\g} \frac{f'}{f} dz$ measures how many times $f(\g)$ goes around 0 for $\g$ closed.

Let $\g$ be a closed path in $\C \setminus\set{0}.$ The winding number or index of $\g$ around 0 is

Note that every closed path in $\C\setminus\set{0}$ is CP-homotopic to one of the paths $\g_n(t) = e^{2\pi i n t}$ for $ n \in \Z$ and $\ind_0 \g_n = \frac{1}{2\pi i} \int_{\g_n} \frac 1z dz = n$ such that $\ind$ is always a natural number.

$\textbf{Lemma 4.2.}$ If $\g$ is a closed path, $f$ holomorphic and nonzero on a neighbourhood of $\g,$ then

$\textit{Proof.}$ This comes out by definitions and chain rule.

Denote $\p D = \coprod P^j$ with $P^j$ disjoint Jordan curves. Then $\ind_0 f\circ \p D = \sum \int_0 f\circ \G^j$ for any Jordan parametrisations that preserve orientation. Let $\D_{\p D} f = 2\pi \int_0 f\circ \p D$ denote the change in argument of $f$ around $\p D.$ We combine our previous theorem and lemma to get the second version of the argument principle.

$\textbf{Theorem 4.3.}$ (Argument Principle version 2) Let $f \in H(\overline{D} \setminus \set{a_1,\ldots,a_n})$ for $D$ a bounded Jordan domain and suppose $f$ has no zeroes on $\p D,$ $a_j$ pole of order $N_j,$ $b_1, \ldots, b_k$ zeroes of order $K_j$ respectively, and $N = \sum N_j,$ $K = \sum K_j.$ Then $\ind_0 f\circ \p D = K - N,$ or equivalently, $\D_{\p D} f = 2\pi (K-N)).$

Let $f \in H(\overline{D}),$ $D$ bounded Jordan domain, $f(z) \not= 0$ on $\p D.$ Then denote $K_{f, D} = \sum_{\text{$b_j$ zero of $j$}} \ord(b_j)$ which count zeroes according to multiplicity. Since $f \in H(\overline{D})$ has no poles, we have $K_{f,D}$ $=$ $\frac 1{2\pi i} \int_{\p D} \frac{f'}{f} dz$ $=$ $\ind_0 f \circ \p D.$

Also note that $f$ has finitely many zeroes in $D.$ This is because $f \in H(U)$ for $\overline{D} \subset U$ compact such that if $f$ had infinitely many zeroes, they would accumulate in $\overline{D}$ such that $f \equiv 0$ by the identity theorem. This is a contradiction since $f$ has no zeroes on $\p D$ by assumption.

We now provide the final piece of the puzzle before proving the open mapping theorem.

$\textbf{Theorem 4.4.}$ (Rouché) Let $f,g \in H(\overline{D})$ with $D$ a bounded Jordan domain. Suppose $|g(z)| < |f(z)|$ on $\p D.$ Then $K_{f,D} = K_{f+g,D}.$

$\textit{Proof.}$ We want to show $\ind_0 f\circ \p D = \int_0 (f+g) \circ \p D,$ or equivalently, $\int_{\p D} \frac{f'}{f} dz = \int_{\p D} \frac{(f+g)'}{f+g} dz.$ Now, if $\g$ is a Jordan parametrisation of a component $\G$ of $\p D,$ we have by our previous lemma $\int_\g \frac{f'}{f} dz = \int_{f\circ \g} \frac 1z dz$ and $\int_\g \frac{(f+g)'}{f+g} dz = \int_{(f+g)\circ \g} \frac 1z dz.$

Now observe that since $|g(z)| < |f(z)|,$ we have a CP-homotopy in $\C \setminus\set{0}$ of $f \circ \g$ and $(f+g) \circ \g$ given by linear interpolation $\G(s,t) = f(\g(t)) + sg(\g(t)).$ Thus, $\int_{f\circ \g} \frac 1z dz = \int_{(f+g)\circ \g} \frac 1z dz.$ So for each component of $\p D,$ we get the same index such that $\ind_0 f \circ \p D = \ind_0 (f+g) \circ \p D.$ $\qed$

An application of Rouché is a proof of the fundamental theorem of algebra. Suppose $p(z)$ $=$ $z^m + a_{m-1}z^{m-1} + \ldots + a_0.$ Let $f(z) = z^m$ and $g(z) = p(z) - f(z).$ Then triangle inequality we can choose $R$ large enough such that $|f(z)|$ $=$ $|z^m|$ $>$ $|g(z)|$ $=$ $|a_{m-1}z^{m-1} + \ldots + a_0|$ on $\p \D(0,R).$ Then $K_{f,\D(0,R)} = K_{z^m, \D(0,R)} = m.$

$\textbf{Theorem 4.5.}$ (Open Mapping Theorem) Let $f \in H(D)$ not constant. Then $f(D)$ is open.

$\textit{Proof.}$ Let $w_0 \in f(D)$ with $f(z_0) = w_0$ for some $z_0 \in D.$ To show that $f(D)$ is open we will find some $\D(w_0,\r) \subset f(D).$ Specifically, we will find $\r, r$ such that $K_{f-w_0, \D(z_0,r)} = K_{f-w,\D(z_0,r)}$ for all $w \in \D(w_0,\r).$ In particular, we want to show $K_{f - w_0, \D(z_0,r)} > 0$ such that $f$ takes $w$ at some point of the disk $\D(z_0,r)$ and hence $w \in f(\D(z_0,r)).$

Since $f$ is not constant, there does not exist a sequence $z_n \in D$ with $f(z_n) = w_0$ and $z_n \to z_0$ by uniqueness theorem. So there eixsts $r > 0$ such that the only $z \in \overline{\D(z_0,r)}$ such that $f(z) = w_0$ is $z_0.$ Let $\r = \min_{z \in \p\D(z_0,r)} |f(z) - w_0|.$ Write $f(z) - w = (f(z)-w_0) + (w_0-w).$ Then for $z \in \p \D(z_0,r),$ $w \in \D(w_0,\r),$ we have $|w_0-w| < \r \leq |f(z) - w_0|$ such that by Rouché we get

which implies $w \in f(\D(z_0,r)) \subset f(D).$ Hence, $\D(w_0, \r) \subset f(D).$ $\qed$

$\textbf{Corollary 4.6.}$ (Maximum modulus principle) If $f \in H(D)$ and $|f|$ has a local maximum in $D,$ then $f$ is constant.

$\textit{Proof.}$ Suppose $f$ is not constant and $|f(z)|$ has a local maximum at $z_0 \in D.$ If $w_0 = f(z_0),$ then $\D(w_0,\r) \subset f(\D(z_0,r))$ for every $r > 0$ small enough by the open mapping theorem. But there exists $w \in \D(w_0,\r)$ such that $|w| > |w_0|.$ This is a contradiction such that $f$ must be constant. $\qed$

$\textbf{Corollary 4.7.}$ (Weak maximum principle) Let $f \in H(D) \cap C(\overline{D}).$ Then $\max_{z \in \overline{D}} |f(z)| = \max_{z \in \p D} |f(z)|.$

$\textit{Proof.}$ In the case the maximum on the boundary we are done. Otherwise, by maximum modulus principle, $f$ is constant so both sides are equal. $\qed$